こんにちは。数学者の妻たーこです。
「わかりやすい高校数学」。
今回は「実数」の第2回です。
今回は小数を見ていこうと思います。
さて,まずは前回やったことを復習しましょう。
自然数+$\color{blue}{\cdots,-3,-2,-1,0}$を整数という。
整数+分数を有理数という。
直線(上の数字)を実数という。
実数から有理数を除いたものを無理数という。
詳しくはこちらをどうぞ。
「小数」とは?
まず上で復習した通り,
数には
自然数,整数,有理数,無理数,実数
がありました。
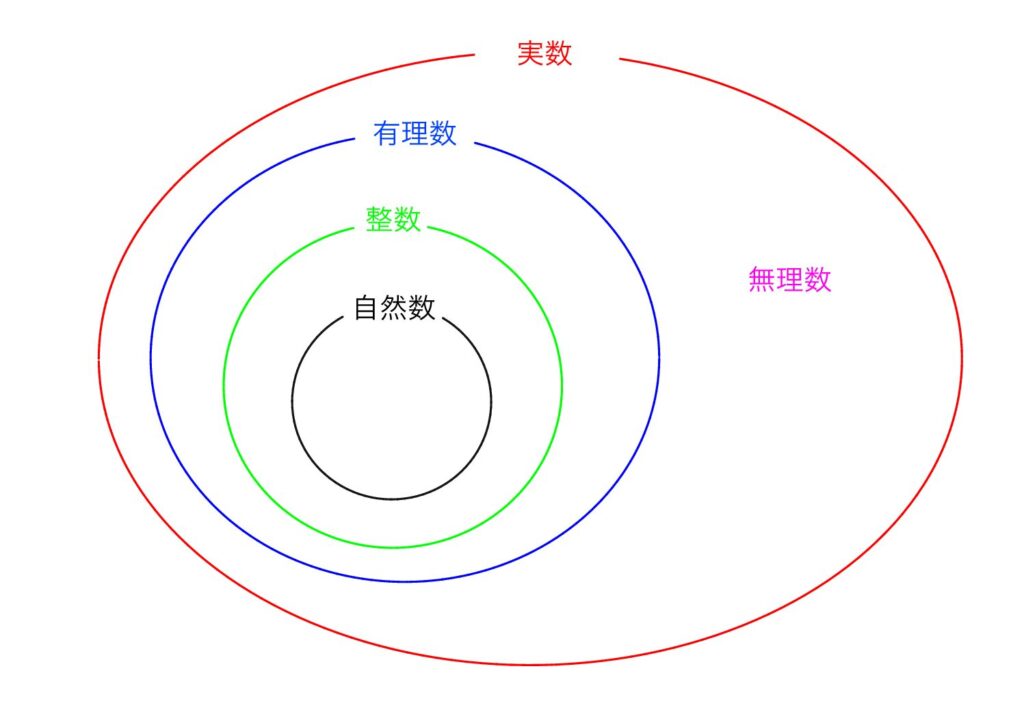
その中で,有理数とは
「分数の形」
をしているものでした。
例えば$\frac{1}{4}$は有理数で,計算すると
$\frac{1}{4}=0.25.$
なので,$\frac{1}{4}$は小数点より下のいくつかの数字でかけます。
(.の下の「2」と「5」のみでかけました。)
では,$\frac{1}{3}$はどうでしょうか?
$$\frac{1}{3}=1\div 3=0.3333333333\cdots$$
となります。
先程の$\frac{1}{4}$と異なり,
今回は小数点の下にずっと数字が続いています。
そこで,
このように小数点の下の数字が限り無く続いてしまうような小数を
無限小数
と言います。
一方,先程の
$\frac{1}{4}=0.25$のように
小数点の下の数字が限り有るので,このような数字を
有限小数
と言います。
では,ここまでをまとめましょう。
1. 小数点以下の数字が限り無く続く小数を「無限小数」という。
2. 小数点以下の数字が限り有る小数を「有限小数」という。
例題1
(1) $\frac{2}{5}$
(2) $\frac{12}{37}$
例題1の解答
(1)
$$\frac{2}{5}=0.4.$$
よって,有限小数。
(2)
$$\frac{12}{37}=0.324324324\cdots.$$
よって,無限小数。
問題1
では,例題にならって,問題を解いてみましょう。
(1) $\frac{3}{11}$
(2) $\frac{2}{19}$
(3) $\frac{3}{2}$
問題1の解答
(1)
$$\frac{3}{11}=0.27272\cdots.$$
よって,無限小数。
(2)
$$\frac{2}{19}=0.10555\cdots.$$
よって,無限小数。
(3)
$$\frac{3}{2}=1.5.$$
よって,有限小数。
無限小数を更に分ける。
さて,問題を解いてみると,
無限小数,つまり,小数点以下が無限に続く小数の中には
$$0.3333\cdots$$
や
$$0.256256256256\cdots$$
のように,同じ数字が何度も何度も繰り返し現れる場合があります。
(かっこよくいうと,循環して現れます。)
そこで,このような無限小数を
循環小数
と言います。
上の例題と問題を見ると全て循環小数ですね。
では,循環しないような小数はあるのでしょうか?
あります。
それは,例えば小学生の時に習った円周率$\pi$です。
$\pi=3.141592653589793\cdots$
などです。
実はこのような循環しない小数のことを
以前に学んだ無理数と言います。
では,まとめましょう。
1. 無限小数の中で,小数点以下のある数字が何度も何度も繰り返し現れるようなものを
循環小数という。
2. 無限小数の中で,循環しないものを無理数という。
例えば,$\frac{1}{3}$は
$\frac{1}{3}=0.333333\cdots$
と何度も何度も同じ数字を書くことになります。
が,面倒ですよね。
数学の世界では,繰り返しの始まりと終わりに$\cdot$をつけて,
簡単に表すことができます。
例えば,
$$0.\color{red}{3}33333\cdots=0.\dot3,$$
$$0.\color{red}{256}256256\cdots=0.\dot25\dot6.$$
などと表すことができます。
では,問題をやって終わりとしましょう。
問題2
例題1と問題1の循環小数を記号$\cdot$を用いて表せ。
問題2の解答
例題1-(2)
$$\frac{12}{37}=0.324324324\cdots=0.\dot32\dot4.$$
問題1-(1)
$$\frac{3}{11}=0.27272\cdots=0.\dot2\dot7.$$
問題1-(2)
$$\frac{2}{19}=0.10555\cdots=0.1\dot5.$$
まとめ
2. 無限小数とは小数点以下が限り無く続く小数
3. 有限小数とは小数点以下が限り有る小数
4. 無限小数は循環小数と無理数に分けられる。
5. 循環小数とは小数点以下のある数字が何度も何度も繰り返し現れるようなもの
6. $0.256256256\cdots=0.\dot25\dot6$などと表す。
今回は小数を学びました。
色々と言葉が出てきましたが,忘れてしまっても大丈夫です。
人間ですから,使わないとすぐ忘れてしまいます。
でも,それを気に病む事はありません。
一度入れておけば取り出すのは簡単なので,
忘れたら,また本やノートやこのページに戻って来ればそれでOKです。
ゆっくり,リラックスして,一緒に数学を学んでいきましょう!



コメント