こんにちは。数学者の妻たーこです。
「わかりやすい高校数学」。
今回は「実数」の第1回です。
私たちはこれまで,
$1,2,3,4,\cdots$
や
$0,-1,-2\cdots$,
$-\frac{13}{5},~\frac{1}{2},~\frac{29}{6},\cdots$,
$-\frac{\sqrt{3}}{5},~\sqrt{2},~\pi,\cdots$
など,たくさんの数字を学んできました。
すると,
「ある数字の集まりには面白い性質があり,
別の数字の集まりにはそのような面白さがない。」
など,数字にも色々な種類があることがわかります。
そこで,
その集まりに名前をつけましょう!
数の集まりに名前をつける
$1,2,3,4\cdots$
などを自然数という。
この自然数に
$\cdots,-3,-2,-1,0$
を加えたものを整数という。
更にこの整数に
$-\frac{13}{5},~\frac{1}{2},~~\frac{29}{6}$
などの分数の形を含めたものを有理数という。
この有理数とは別の
$-\frac{\sqrt{3}}{5},~~\sqrt{2},~~\pi$
などの数を無理数という。
最後に,この有理数と無理数を合わせたものを
実数という。
… と言ってもわかりにくいので,絵や,図でかいてみます。
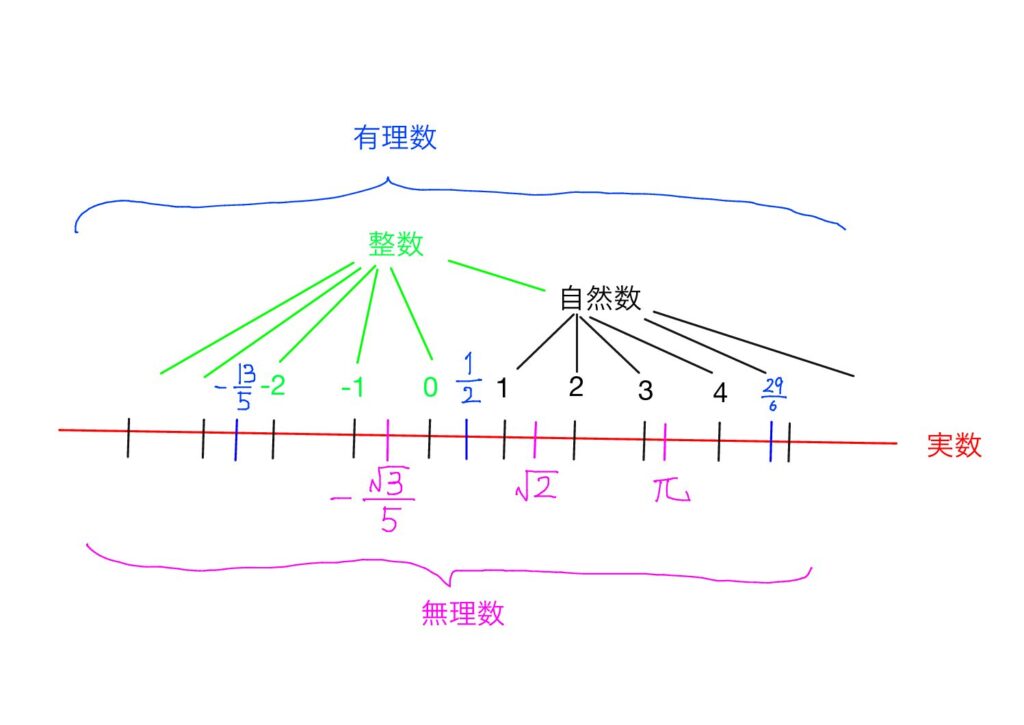
絵を説明してみます。
- 実数というのは定規で書いたまっすぐな線,つまり,直線のことです。
- その実数は「有理数(分数の形でかける数字)」と無理数に分けられます。
- 有理数の中で,分数の形でない$-3,0,5$などを整数と言います。
- 整数の中で,$1,2,3$などの数字を自然数と言います。
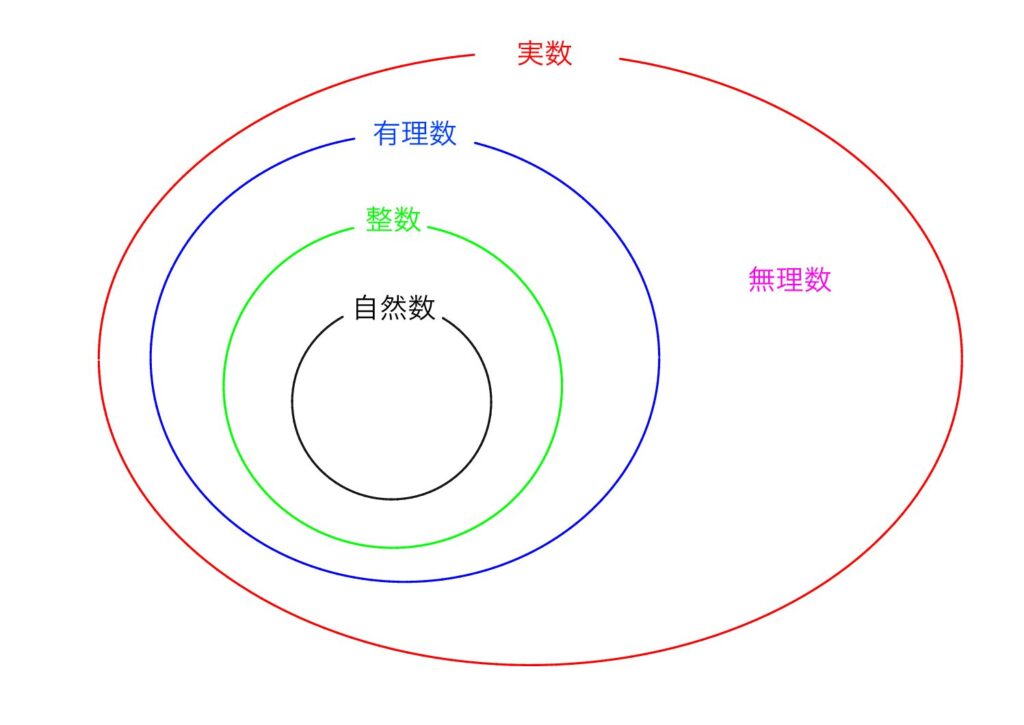
この図の方が実数は有理数と無理数に分けられて,
有理数の中に整数があり,整数の中に自然数があることが分かると思います。
では,問題を解いてみましょう。
問題1
1. $-1$は整数である。
2. $1$は整数である。
3. $5$は無理数である。
4. $\frac{1}{3}$は有理数である。
5. $\sqrt{2}$は実数である。
問題1の解答
1. 「$-1$は整数である。」は正しい。(○)
2. 「$1$は整数である。」は正しい。(○)
実際,$1$は自然数で,特に整数ですね。
3. 「$5$は無理数である。」は正しくない。(X)
実際,$5$は整数で,特に有理数です。
無理数は実数の中で,有理数でないものなので,
(文章がわかりにくいと感じたら,上の絵をみましょう。)
有理数である$5$は無理数ではないですね。
4. 「$\frac{1}{3}$は有理数である。」は正しい。(○)
実際,分数の形なので,有理数ですね。
5. 「$\sqrt{2}$は実数である。」は正しい。(○)
実際,$\sqrt{2}$は無理数で,特に,実数です。
例題1
$a,~b$を自然数とする。
このとき,$a\div b=\frac{a}{b}$は自然数にはならないことがある。
その例を挙げよ。
例題1の解答
例を挙げる。
$a=1, b=2$とする。
すると,
$$1\div 2=\frac{1}{2}$$
となる。これは分数の形をしているので,自然数ではない。
問題2
では,問題を解いてみましょう。
(1) $a,~b$を自然数とする。
このとき,$a-b$は自然数にならないことがある。
その例を挙げよ。
(2) $a,~b$を整数とする。ただし,$b\not=0$とする。
このとき,$a\div b$は整数にならないことがある。
その例を挙げよ。
(3) $a,~b$を自然数とする。
このとき,$a\div b=\frac{a}{b}$は自然数にはならないことがあることを例題で学んだ。
一方で,自然数になることもある。その例を挙げよ。
問題2の解答
例を挙げる。
(1) $a=2,~b=5$とおく。
このとき,
$$a-b=2-5=-3.$$
$-3$は自然数でないので,これが例となる。
(2) $a=-3,~b=4$とおく。
このとき,
$$a\div b=-3\div 4=-\frac{3}{4}.$$
これは分数の形をしているので,これが例となる。
(3) $a=9,~b=3$とおく。
このとき,
$$a\div b=9\div 3=3.$$
これは自然数であるので,これが例となる。
他の場合は引き算,割り算はどうなるの?
例題と問題を通して,
自然数,整数,有理数,実数の中で,
自然数は引き算をすると自然数にならないことがありました。
自然数,整数は割り算をするとそれぞれ自然数,整数にならないことがありました。
では,他の場合はどうかというと次のようになります:
自然数の場合
$a,b$を自然数とします。
このとき,
$a+b:$ 自然数
$a-b:$ 自然数にならないことがある。
$a\times b:$ 自然数
$a\div b:$ 自然数にならないことがある。
整数の場合
$a,b$を整数とします。
このとき,
$a+b:$ 整数
$a-b:$ 整数
$a\times b:$ 整数
$a\div b:$ 整数にならないことがある。
有理数の場合
$a,b$を有理数とします。
このとき,
$a+b:$ 有理数
$a-b:$ 有理数
$a\times b:$ 有理数
$a\div b:$ 有理数
実数の場合
$a,b$を実数とします。
このとき,
$a+b:$ 実数
$a-b:$ 実数
$a\times b:$ 実数
$a\div b:$ 実数
つまり,例題と問題でやったものだけ,
ちょっと変なことが起きていることがわかります。
無理数は!?
無理数の場合はちょっと特殊で,しかも,難しいです。
例えば,無理数+無理数が有理数になったります。
もしかすると,高校の先生も知らない内容かもしれません。
興味があれば,本を読んでみることをお勧めします。
まとめ
自然数+$\color{blue}{\cdots,-3,-2,-1,0}$を整数という。
整数+分数を有理数という。
直線(上の数字)を実数という。
実数から有理数を除いたものを無理数という。
この内容は「ちゃんとやろう」と思うより,
数字を楽しもうと思った方が身につくと思います。
図や,表や絵をかいてゆっくり楽しんでいきましょう!



コメント