【実数】絶対値 わかりやすく 解説

こんにちは。数学者の妻たーこです。
「わかりやすい高校数学」。

今回は「実数」の第3回です。

今回は「絶対値」を見ていこうと思います。

絶対値はこの先よく出てくる内容で，

大学入試にも本当によく出てきます。

数学者の夫曰く，

とのことです。

数直線

まずは，言葉の確認から始めましょう。

まず，前回次のことを学びました。

そこで，この実数を表す直線のことを

数直線

と言います。

また，点Oを原点と言います。

また，数直線上の点$A$が$a$という値の時，

$A(a)$

などと書きます。

点までの長さ

では，次に原点Oからそれぞれの点までの長さを表してみましょう。

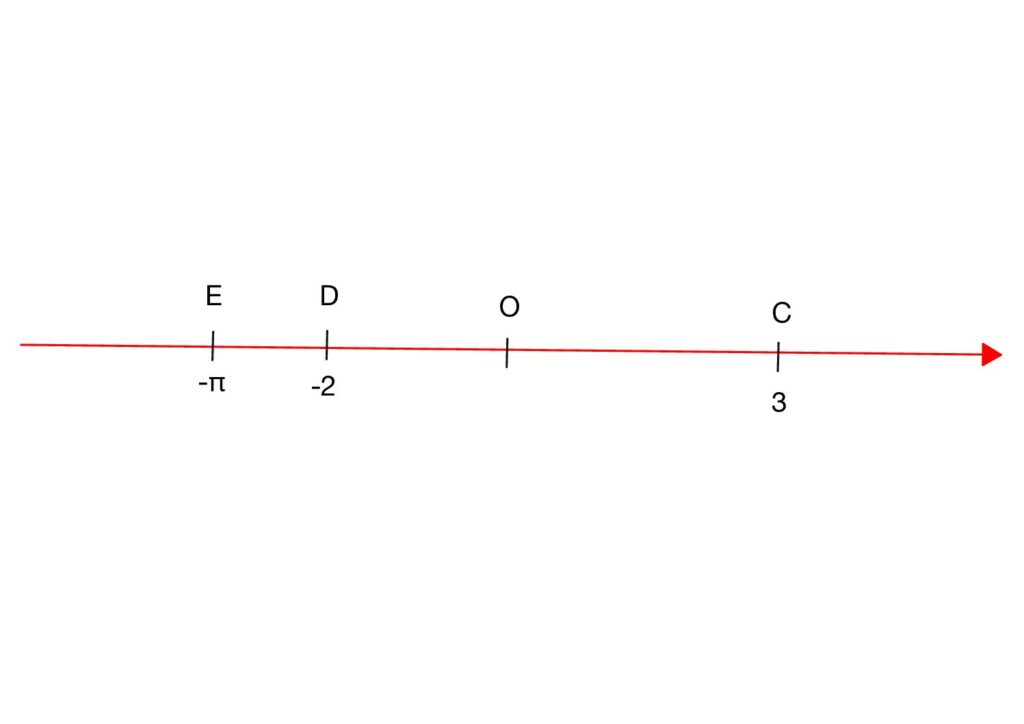
原点Oから$C(3)$までの長さは3ですね。

原点Oから$D(-2)$までの長さは2ですね。

原点Oから$D(-\pi)$までの長さは$\pi$ですね。

このように，

原点からその点までの長さ（距離）を表すものを

絶対値と言います。

そして，次のように書きます。

$$|3|=3,$$

$$|-2|=2,$$

$$|-\pi|=\pi.$$

つまり，絶対値とは

+のものはそのまま+にし，

-のものは+にする

ようなもののことをいいます。

なお，原点から原点までの距離は0なので，

$$|0|=0$$

です。

問題1

では，問題を解いていきましょう！

問題1の解答

(1) $|4|=4,$
(2) $|-3|=3,$
(3)$|-0.22|=0.22.$

実は絶対値は難しい

さて，ここまでみると，

「絶対値なんて簡単だ。」

と思うのですが，

実はちょっと頭を使うシーンが出てきます。

では，もう1度絶対値を確認してみましょう。

$$|-1|=1,$$

$$|-3|=3,$$

$$|-10|=10,$$

$$|-66|=66.$$

ですね。

では，

$$|a|=a$$

でしょうか？

なんとなく正しいような気がしてしまいますが，

実は違います。

実際，上の例を見てみましょう。

$a=-1$とすると，

$$|a|=|-1|=1\not=-1=a$$

となっていますね。

つまり，$a$がマイナスの時は$|a|=a$ではなく，

$$|\color{blue}{a}|=-\color{blue}{a}$$

となるわけです。

つまり，

文字の絶対値を外すときはよく考えないといけない

ということがわかると思います。

ちゃんと説明すると，

次のようになるのですが，

これは覚えなくていいです。

なぜなら，これを覚えよう覚えようとすると，

難しい問題にであったときに，

「絶対値の性質を覚えていないから解けないんだ」

と思ってしまって，解くのをやめてしまうからです。

ですので，絶対値は

文字の絶対値を外すときはよく考えないといけない

というちょっと曖昧な感じを持っているだけでいいです。

そして，その都度考えて答えを出すようにしましょう。

例題1

例題2の解答

$3-\pi<0$ なので，

$$|3-\pi|=\pi-3.$$

問題2

では，最後に問題を解いていきましょう。

問題2の解答

(1) $\sqrt{2}-2<0$ より，
$$|\sqrt{2}-2|=2-\sqrt{2}.$$

(2) $\pi-10<0$ より，
$$|\pi-10|=10-\pi.$$

(3) $a>3$, $0<b<2$ なので，
（例えば，$a=4,~b=1$ なので，$b-a=1-4=-3<0$ となる。）
$b-a<0$
となる。よって，
$$|b-a|=a-b.$$

まとめ

今回は絶対値を学びました。

なんとなく，わかった気になれば今のところOKです。

では，これからも数学を楽しんでいきましょう。