【式の計算】因数分解2 わかりやすく解説

こんにちは。数学者の妻たーこです。
「わかりやすい高校数学」。

今回は「式の計算」の【因数分解】の第2回です。

【この記事を読むと分かること】
1. $x,~y$を含む2次式の因数分解の方法
2. $5x^2-12x+4$などの形の因数分解の方法

前回は $x^2+3x+2$ などの
「$x$などの文字1つ」
と
「数字」
のみで書かれた式の因数分解ができるようになりました。

では，
$$x^2+3xy+2y^2$$
などの文字が２つ入った場合は
どのように因数分解するのでしょうか？

答えは簡単で，
「$y$ は数字と思って因数分解する」
だけでいいです。

では，一緒に見ていきましょう！

例題1
問題1
問題1の解答
$ 5x^2-12x+4 $の形の因数分解
問題2
問題2の解答
２つの問題を合わせた問題
問題の解答
まとめ

例題1

例題1　次の式を因数分解せよ。
$$x^2+3xy+2y^2$$

$$x^2+3x+2$$
を因数分解した時と同じように，
表を書くと，

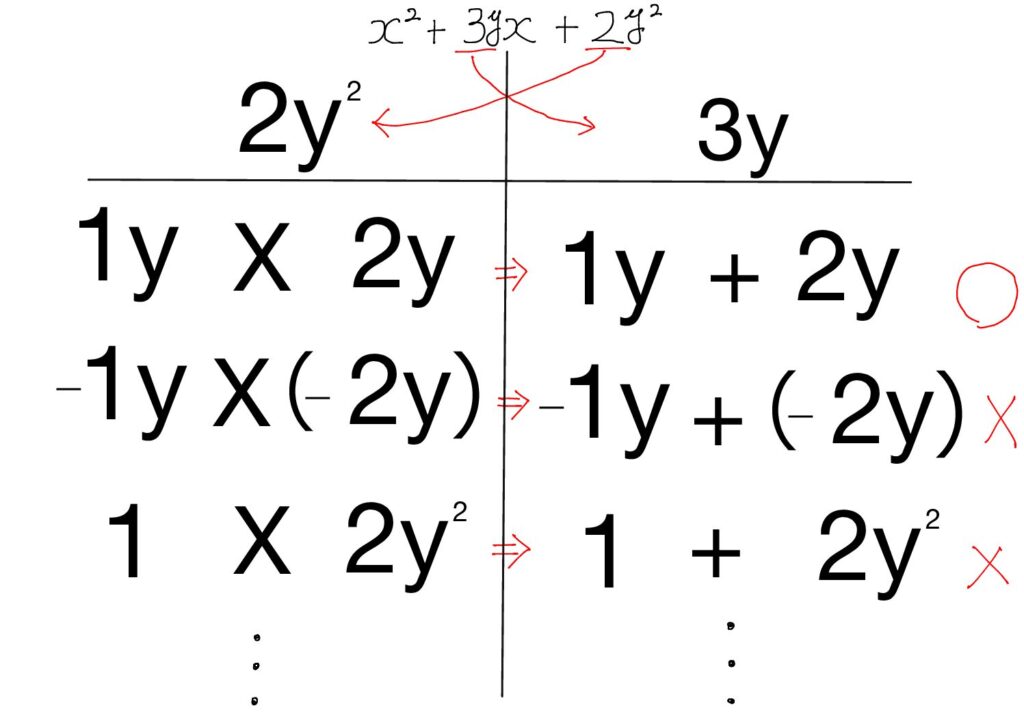
よって，

$$x^2+3xy+2y^2=(x+y)(x+2y)$$

となります。

実際に，右辺を展開して確かめてみましょう。

\begin{align*}
(x+y)(x+2y)
=&~x\cdot x+x\cdot 2y+y\cdot x+y\cdot 2y\\
=&~x^2+2xy+xy+2y^2\\
=&~x^2+3xy+2y^2.
\end{align*}

確かに $x^2+3xy+2y^2$ を因数分解すると
$(x+y)(x+2y)$ になることが確かめられましたね。

問題1

問題1 次の式を因数分解せよ。
(1) $x^2-3xy-18y^2$
(2) $x^2+6xy+8y^2$

問題1の解答

例題と同じで，表を書いて答えていきましょう！

(1)
\begin{align*}
x^2-3xy-18y^2
=&~x^2+(-6y+3y)x+(-6y)\cdot 3yx \\
=&~(x-6y)(x+3y).
\end{align*}

(2)
\begin{align*}
x^2+6xy+8y^2
=&~x^2+(4y+2y)x+4y\cdot 2yx \\
=&~(x+4y)(x+2y).
\end{align*}

$ 5x^2-12x+4 $の形の因数分解

この因数分解はどうやって求めるのでしょうか？

一緒に考えていきましょう！

先ほどまでの因数分解は
$$x^2+3x+2=(x+2)(x+1)$$
と
$$x^2+\color{red}{\triangle} x+\color{red}{\bigcirc}=(x+\color{red}{\square})(x+\color{red}{\star})$$
の形をしていました。

つまり，
$$x^2+(b+d)x+bd=(x+b)(x+d)$$
の形を考えていたわけです。

今回は$x^2$の前にも数字があるので，

$$(ax+b)(cx+d)$$
の形を考えてみましょう。

これを展開すると

\begin{align*}
(ax+b)(cx+d)
=&~ax\cdot cx+ax\cdot d+b\cdot cx +b\cdot d\\
=&~acx^2+adx+bcx +bd\\
=&~acx^2+(ad+bc)x+bd.
\end{align*}

となります。

つまり，

$$\color{red}{ac}x^2+(\color{blue}{ad+bc})x+\color{green}{bd}=(ax+b)(cx+d)$$

なので，

$$\color{red}{5}x^2\color{blue}{-12}x+\color{green}{4}$$

を因数分解するには，

\begin{cases}
\color{red}{ac}=\color{red}{5}\\
\color{blue}{ad+bc}=\color{blue}{-12}\\
\color{green}{bd}=\color{green}{4}\\
\end{cases}

となるように $a,b,c,d$ を決めることができれば良いことがわかります。

そこで，次のように表を書きましょう。

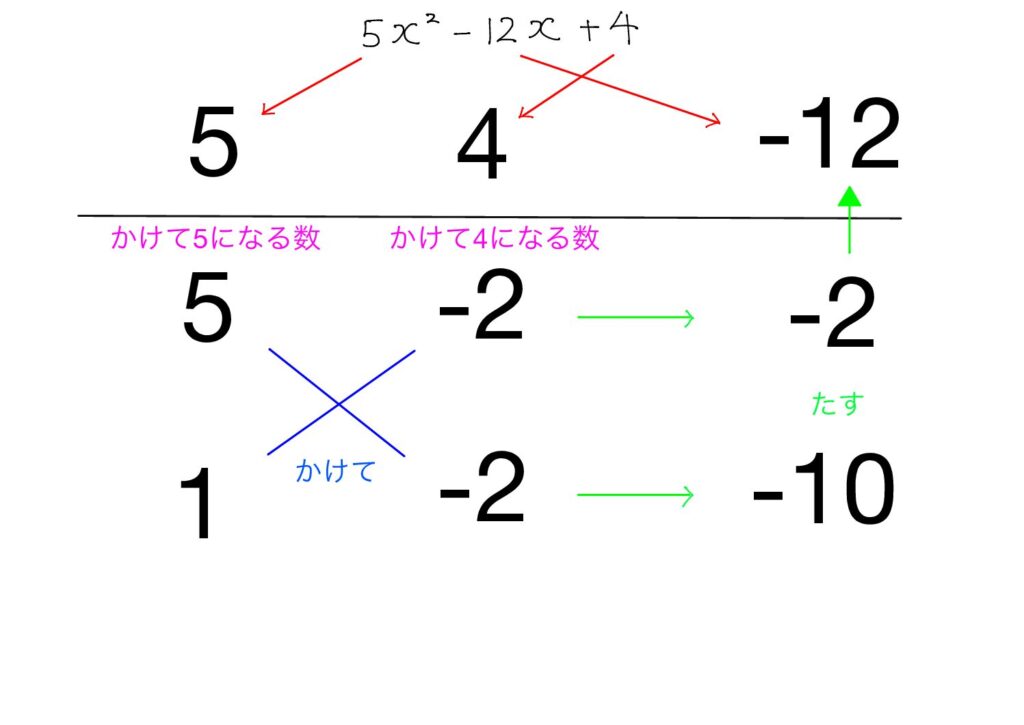
方法は次の通りです：

赤い矢印の通りに数字を書く（5,4,-12を書く）
「5」，「4」を分解して斜めにかける（5を5,1に4を-2,-2に分解して斜めにかける）
かけて出た２つの答えを足す（-2+(-10)をする）
出てきた答えが右の一番上と同じものになるか確認する(-2-10が-12になることを確認)
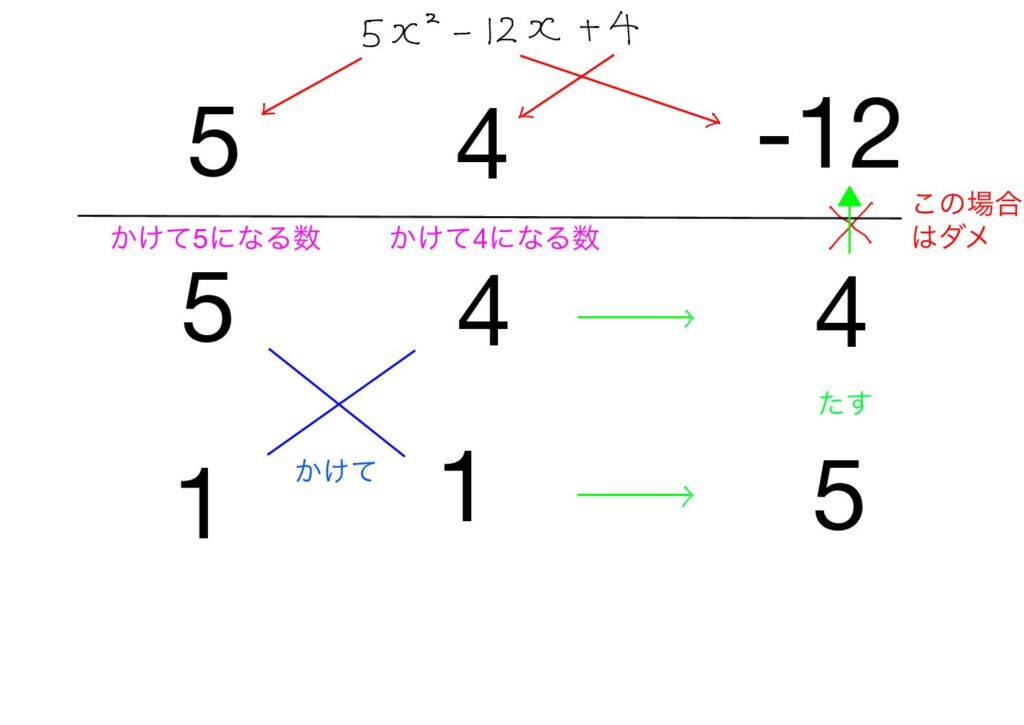
ダメなら，「2」からやり直す。（上の例はOK!!）

下の例は間違ってしまっている例です。

足し算よりも引き算の方が難しく，

掛け算よりも割り算の方が難しいように，

展開よりも因数分解の方が難しいです。

ですので，「パッ」と答えが出なくても大丈夫です。

それより，ゆっくり丁寧に考えて答えに辿り着ければいいです。

問題2

問題2 次の式を因数分解せよ。
(1) $5x^2+13x+6$
(2) $8x^2+2x-3$

問題2の解答

例題と同じように，表を書いて答えていきましょう。
(1)
\begin{align*}
5x^2+13x+6
=&~ (5x+3)(x+2).
\end{align*}

(2)
\begin{align*}
8x^2+2x-3=(4x+3)(2x-1).
\end{align*}

合っているか不安なら，展開すればいいですね。

実際に計算練習になるので，一緒に展開してみましょう。

問題2の解答が合っているか確かめ

(1) $(5x+3)(x+2)$ を展開すると，
元の式，
$5x^2+13x+6$
になることを確かめる。

\begin{align*}
(5x+3)(x+2)
=&~5x^2+10x+3x+6\\
=&~5x^2+13x+6.
\end{align*}

(2) $(4x+3)(2x-1)$ を展開すると，
元の式，
$8x^2+2x-3$
になることを確かめる。

\begin{align*}
(4x+3)(2x-1)
=&~8x^2-4x+6x-3\\
=&~8x^2+2x-3.
\end{align*}