【式の計算】因数分解4 わかりやすく 解説

こんにちは。数学者の妻たーこです。
「わかりやすい高校数学」。

今回は「式の計算」の【因数分解】の第4回です。

問題1

問題1の解答

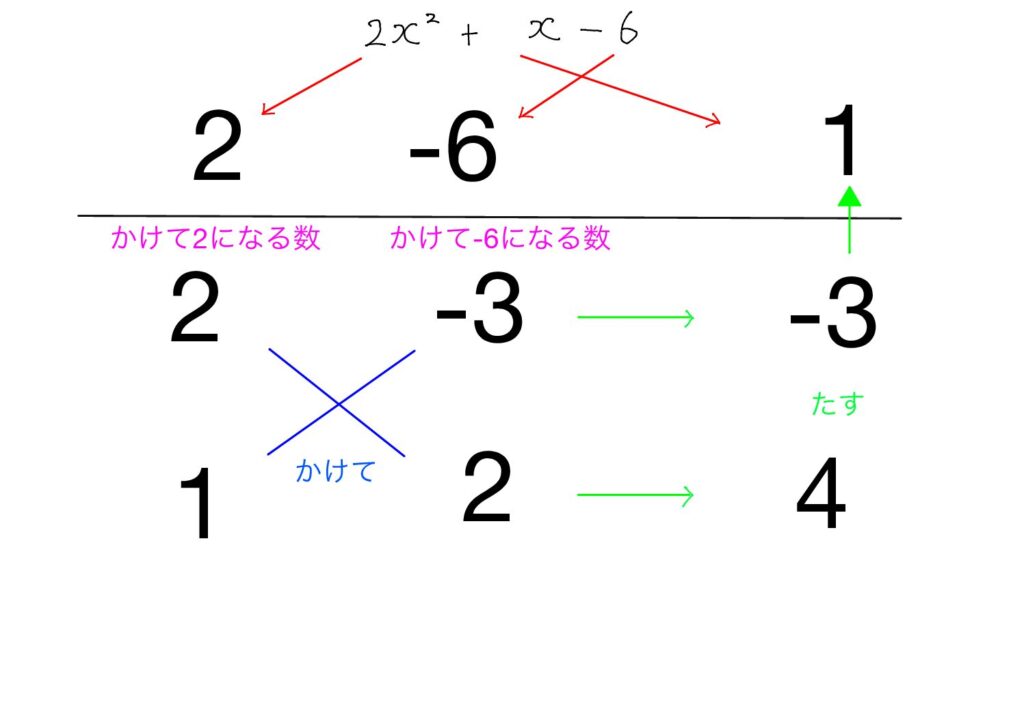
よって，
$$2x^2+x-6=(2x-3)(x+2).$$

問題2

では，いよいよ今回の問題を解いていきましょう。

問題2の解答

\begin{align*}
2x^2+3\color{red}{x}y+y^2+\color{red}{x}-y-6
=&~2x^2+(3y+1)x+y^2-y-6~~(x\text{でまとめる})\\
=&~2x^2+(3y+1)x+(y+2)(y-3)~~(y^2-y-6\text{を因数分解してみる})
\end{align*}

よって，
\begin{align*}
2x^2+3xy+y^2+x-y-6
=&~(2x+y+2)(x+y-3).
\end{align*}

この問題も結局これまでに学んだ
「$ax^2+bx+c$の形の因数分解」
と
「$y$を数字だと思う因数分解」
をすればいいだけですね。

では，演習問題を１問やってみましょう。

問題3

問題3の解答

$$6x^2+(5y+1)x+y^2-1=(3x+y-1)(2x+y+1).$$

問題4

では，今日最後の問題です。

その前に，次の因数分解をしてみましょう。

$$X^2+3X+2$$

簡単でしたでしょうか？

答えは（いつものように表を書いて）

$X^2+3X+2=(X+2)(X+1)$

ですね。

では，いよいよ問題です。

問題4の解答

$\color{red}{X=x^2}$とおく。

\begin{align*}
x^4+3x^2+2
=&~X^2+3X+2\\
=&~(X+2)(X+1)\\
=&~(x^2+2)(x^2+1)
\end{align*}

この問題はこれ以上因数分解できないので，
これが答えになります。
（多くの問題ではもう少し因数分解できる形になっています。）

また，この問題は
「結局，$X^2+3X+2$の因数分解」
を解くことと同じであることがわかります。

つまり，
次数の高い因数分解も
結局はこれまでに学んだ因数分解を考えればよいだけだ
ということがわかります。

では，演習問題を解いてみましょう。

問題5

問題5の解答

$X=x^2$とおく。

\begin{align*}
8x^4+10x^2-3
=&~8X^2+10X-3\\
=&~(4X-1)(2X+3)\\
=&~(\color{red}{4x^2-1})(2x^2+3)\\
=&~(2x+1)(2x-1)(2x^2+3).
\end{align*}

先ほどの問題と違い，この問題では$4x^2-1$の部分がもう少し因数分解できますので，
$(2x+1)(2x-1)$まで分解した上の形が答えになります。

今は

「結局どこまで因数分解すればいいのかわからない！」

と思うかもしれませんが，

因数分解は基本的に「方程式を解くとき」，

に使いますので，

自然とどこまで因数分解すればいいかがわかります。

そのため，

とりあえずの中間試験や期末試験では

できるだけ$x$の1次式（つまり，$x^\triangle$の$\triangle$が1）

になるように因数分解をするようにして，

できなさそうならその前で止めれば大丈夫です。

まとめ

皆さんお疲れ様でした。

これからも一緒に数学を楽しんでいきましょう。