こんにちは。数学者の妻たーこです。
「わかりやすい高校数学」。
今回は「式の計算」の【因数分解】です。
因数分解は役に立つ
まず,次の問題を見てみよう!
Q. $(x-3)(x-2)=0$
を解け。
これは
$x-3=0$, $x-2=0$
つまり,
$x=3,~~x=2$
ですよね。
では,次の問題はどうでしょうか?
Q. $x^2-5x+6=0$
を解け。
この問題はさっきと違いすぐに答えが出ません。
ですが,実は,この式は先程の式
$$(x-3)(x-2)=0$$
と同じです。
実際に同じになることを計算してみましょう!
$$(x-3)(x-2)=x^2+(-3-2)x+(-3)(-2)=x^2-5x+6$$
で確かに同じになります。
ということは,
「展開」したものを「元に戻す操作」
ができれば方程式の答え(ここでは $x^2-5x+6=0$ を解いた答え)
がすぐに分かるわけです。
そこで,この
【展開したものを元に戻す操作】
が大切だと分かります。
これが「因数分解」です。
次に,
【多項式の中に同じ文字や数字があればそれをカッコの外側に出して】
見やすくしてみましょう!
例題1
(1)
\begin{align*}
ab+ac+ad
=&~\color{red}{a}b+\color{red}{a}c+\color{red}{a}d\\
=&~\color{red}{a}(b+c+d)
\end{align*}
(2)
\begin{align*}
2xy-y
=&~2x\color{red}{y}-\color{red}{y}\\
=&~\color{red}{y}(2x-1)
\end{align*}
(3)
\begin{align*}
4x^2y-2xy^2
=&~\color{red}{2}2x^2y-\color{red}{2}xy^2\\
=&~2(2\color{red}{x}xy-\color{red}{x}y^2)\\
=&~2x(2xy-y^2)\\
=&~2x(2x\color{red}{y}-\color{red}{y}y)\\
=&~2xy(2x-y)
\end{align*}
もしくは
\begin{align*}
4x^2y-2xy^2
=&~\color{red}{2xy}2x-\color{red}{2xy}y\\
=&~2xy(2x-y)
\end{align*}
問題1
(1) $xy+xz$
(2) $2a^2b+ab$
(3) $x^2y+xy^2$
問題1の解答
(1)
\begin{align*}
xy+xz
=&~\color{red}{x}y+\color{red}{x}z\\
=&~x(y+z).
\end{align*}
(2)
\begin{align*}
2a^2b+ab
=&~2\color{red}{ab}a+\color{red}{ab}\\
=&~ab(2a+1).
\end{align*}
(3)
\begin{align*}
x^2y+xy^2
=&~\color{red}{xy}x+\color{red}{xy}y\\
=&~xy(x+y).
\end{align*}
因数分解のための方法
次は方程式を解くための因数分解の方法を見ていきます。
まず,次の式はとても重要なので,復習しておきましょう!
実際に計算して確かめてみましょう。
\begin{align*}
(x+a)(x+b)
=&~x\cdot x+x\cdot b+a\cdot x+a\cdot b\\
=&~x^2+b x+ax+ab\\
=&~x^2+(a+b)x+ab\\
\end{align*}
例題2
$$x^2+3x+2$$
を因数分解せよ。
まず,
$$x^2+3x+2$$
に対して,下の表を書きましょう。
そして,次のようにして,
因数分解した後の形 $(x+a)(x+b)$ の数字 $a,~b$ を探します。
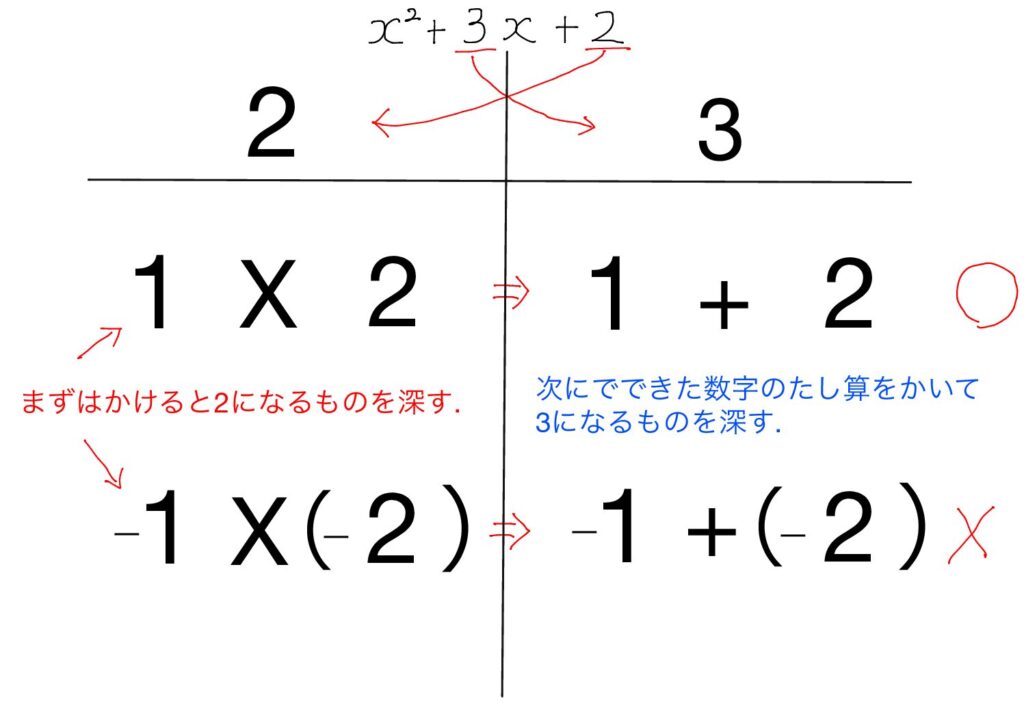
ここで,出てくる数字,$1,~2$ が $a,~b$ となります。
つまり,
$$x^2+3x+2=(x+1)(x+2)$$
となります。
問題2
(1) $x^2+6x+9$
(2) $x^2-10x+21$
(3) $x^2+5x-24$
問題2の解答
それぞれ,上の表を書いて答えていきましょう。
(1)
\begin{align*}
x^2+6x+9
=&~x^2+(3+3)x+3\cdot3\\
=&~(x+3)(x+3)\\
=&~(x+3)^2.
\end{align*}
(2)
\begin{align*}
x^2-10x+21
=&~x^2+(-7-3)x+(-7)\cdot(-3)\\
=&~(x-7)(x-3).
\end{align*}
(3)
\begin{align*}
x^2+5x-24
=&~x^2+(8-3)x+8\cdot(-3)\\
=&~(x+8)(x-3).
\end{align*}
まとめ
(2) 因数分解はある程度は型にはまったやり方でできる



コメント