こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

軌跡を勉強しよう!
軌跡の解き方を勉強したい人はこちらも参照

問題
実数 $m$ が次の条件を満たしながら変化するとき,次の点 $P$ の軌跡を求めよ。
$m>0$のとき,放物線 $y=2x^2-2mx+m^2-4m+5$ の頂点$P$
実数 $m$ が次の条件を満たしながら変化するとき,次の点 $P$ の軌跡を求めよ。
$x^2+y^2-2(m-1)x+4my+4(m^2+1)=0$ が円を表すときの中心 $P$
解答例
問題1の解答
求める点$P$を $(X,Y)$ とおく。
\begin{align*}
y
=&~ 2x^2-2mx+m^2-4m+5\\
=&~ 2\big(x-\frac{m}{2}\big)^2-2\frac{m^2}{4}+m^2-4m+5\\
=&~ 2\big(x-\frac{m}{2}\big)^2+\frac{m^2}{2}-4m+5
\end{align*}
よって,
\begin{equation}\tag{1}
X=\frac{m}{2},
\end{equation}
\begin{equation}\tag{2}
Y=\frac{m^2}{2}-4m+5.
\end{equation}
$m>0$ より,$X>0$.
$(1)$ より,$m=2X$.
これを $(2)$ に代入して
\begin{align*}
Y
=&~ \frac{(2X)^2}{2}-4(2X)+5\\
=&~ 2X^2-8X+5\\
=&~ 2(X-2)^2-2\cdot4+5\\
=&~ 2(X-2)^2-3
\end{align*}
よって,求める点$P$の軌跡は
$$y=2(x-2)^2-3$$
ただし,$x>0$ の部分。
問題2の解答

もう一度問題を確認
実数 $m$ が次の条件を満たしながら変化するとき,次の点 $P$ の軌跡を求めよ。
$x^2+y^2-2(m-1)x+4my+4(m^2+1)=0$ が円を表すときの中心 $P$
求める点 $P$ を $(X,Y)$ とおく。
$$x^2+y^2-2(m-1)x+4my+4(m^2+1)=0$$
が円を表すので,変形する。
\begin{align*}
(x-(m-1))^2-(m-1)^2+(y+2m)^2-4m^2+4(m^2+1)&=0,\\
(x-(m-1))^2+(y+2m)^2-m^2+2m-1-4m^2+4m^2+4&=0,\\
(x-(m-1))^2+(y+2m)^2-m^2+2m+3&=0,\\
(x-(m-1))^2+(y+2m)^2=m^2-2m-3.
\end{align*}
これが円を表すので,
$$m^2-2m-3>0.$$
よって,
$$(m-3)(m+1)>0.$$
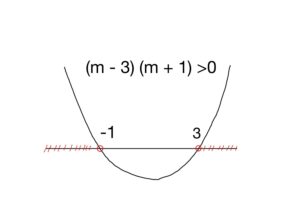
よって,
\begin{equation}\tag{3}
m<-1,~~3<m.
\end{equation}
$(X,Y)$ は円の中心より,
$$X=m-1,~~Y=-2m.$$
よって,
$m=X+1$ を $Y=-2m$ に代入して,
$$Y=-2(X+1)=-2X-2.$$
ここで,$(3)$ より,
$$X+1<-1,~~3<X+1.$$
よって,
$$X<-2,~~2<X.$$
よって,求める点 $P$ の軌跡は
$$y=-2x-2,$$
ただし,$x<-2,~~2<x$の部分。
今日のポイント
2. 実数 $m$ の条件から方程式が存在する範囲が出てくることがあるので,そこに注意!

例えば今日の問題2だと
$m<-1,~~3<m$
から
$x<-2,~~2<x$
が出てきたね!
頭を良くしたいならDHAがおすすめです↓



