【高校数学の分かりやすいサイト】問題解説「三角関数6」

こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう！

たーこ

今日は三角関数の問題です。
今日は２問!

問題

解答

問題1の解答

$$2\sin^2\theta+5\cos\theta-4<0$$
は $\sin\theta,~\cos\theta$ を含んでいるので，
$$\sin^2+\cos^2\theta=1$$
を用いて $\cos\theta$ のみにする。
$$\sin^2\theta=1-\cos^2\theta$$
を代入して，
$$2(1-\cos^2\theta)+5\cos\theta-4<0.$$
よって，
$$-2\cos^2\theta+5\cos\theta-2<0.$$
よって，
$$2\cos^2\theta-5\cos\theta+2>0.$$
よって，
$$(2\cos\theta-1)(\cos\theta-2)>0.$$
よって，
$$2(\cos\theta-\frac{1}{2})(\cos\theta-2)>0.$$

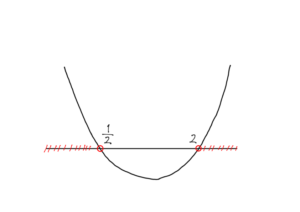
図より，
$$\cos\theta<\frac{1}{2},~~~~~2<\cos\theta.$$
ここで，$\cos\theta\leqq1$ より
$$2<\cos\theta$$
は不適。
よって，
$$\cos\theta<\frac{1}{2}.$$

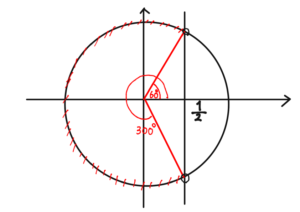
図より，
$$60^\circ<\theta<300^\circ.$$

問題2の解答

たーこ

問題をもう1度確認。

問題2の解答
$$\cos\theta-\sin^2\theta=\alpha$$ 
は $\sin\theta,~\cos\theta$ を含んでいるので，
$$\sin^2+\cos^2\theta=1$$
を用いて $\cos\theta$ のみにする。
$$\sin^2\theta=1-\cos^2\theta$$
を代入して，
$$\cos\theta-(1-\cos^2\theta)=\alpha.$$ 
よって，
$$\cos^2\theta+\cos\theta-1=\alpha.$$
$t=\cos\theta$ とおく。
$$-1\leqq\cos\theta\leqq1$$ 
より，
$$-1\leqq t \leqq1.$$
よって，
$$t^2+t-1=\alpha$$ 
が $-1\leqq t \leqq1$ の範囲で解を持てばよい。
\begin{align*}
y
=& t^2+t-1\\
=& \left(t-\frac{1}{2}\right)^2-\frac{5}{4}
\end{align*}

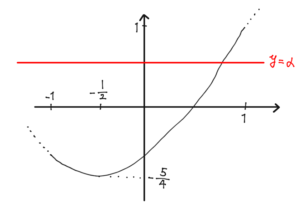
図より，
$$y=t^2+t-1~~\text{と}~~y=\alpha$$
が交わるのは
$$-\frac{5}{4}\leqq\alpha\leqq 1.$$