こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

今日は加法定理の問題です。
加法定理は覚えておかないといけないけど,
それ以外はその都度導くようにしよう!
問題
$x$ の方程式
$$\cos2x+2k\sin x+k-4=0$$
が $0^\circ\leqq x \leqq180^\circ$
の範囲で異なる2つの解を持つための $k$ の条件を定めよ。
解答
まず,$\cos2x+2k\sin x+k-4=0$
には $\cos2x$, $\sin x$ が含まれているので,
$\cos2x$ を変形して,$\sin x$のみの式にする。
加法定理
$$\cos(a+b)=\cos a\cos b-\sin a\sin b$$
より,$b=a$ とおくと,
\begin{align*}
\cos 2a
=&~\cos a\cos a-\sin a\sin a\\
=&~\cos^2 a-\sin^2 a
\end{align*}
ここで,$\sin^2a+\cos^2a=1$
より,
\begin{align*}
\cos 2a
=&~(1-\sin^2a)-\sin^2 a\\
=&~-2\sin^2 a+1
\end{align*}
よって,
$$\cos2x+2k\sin x+k-4=0$$
は
$$-2\sin^2 x+1+2k\sin x+k-4=0,$$
$$-2\sin^2 x+2k\sin x+k-3=0.$$
ここで,
$t=\sin x$
とおくと,
$$-2t^2+2kt+k-3=0.$$
ここで,
$0^\circ\leqq x \leqq180^\circ$ より,
$0\leqq t\leqq 1.$
ここで,
$t=\sin x=1$ のときは
$x=90^\circ$
とただ1つの解を持つが,
それ以外で $t$ が解を1つ持つと
$x$ は解を2つ持つ。
よって,
$$y=f(t)=-2t^2+2kt+k-3$$
とおいて,これが
$0\leqq t<1$
で解をただ1つ持つときを求めればよい。
\begin{align*}
y=f(t)
=&~-2t^2+2kt+k-3\\
=&~-2\Big(t-\frac{k}{2}\Big)^2-2\frac{k^2}{4}+k-3\\
=&~-2\Big(t-\frac{k}{2}\Big)^2-\frac{k^2}{2}+k-3
\end{align*}
これは次のいずれかの場合が考えられる。
(1) 図のように接するとき
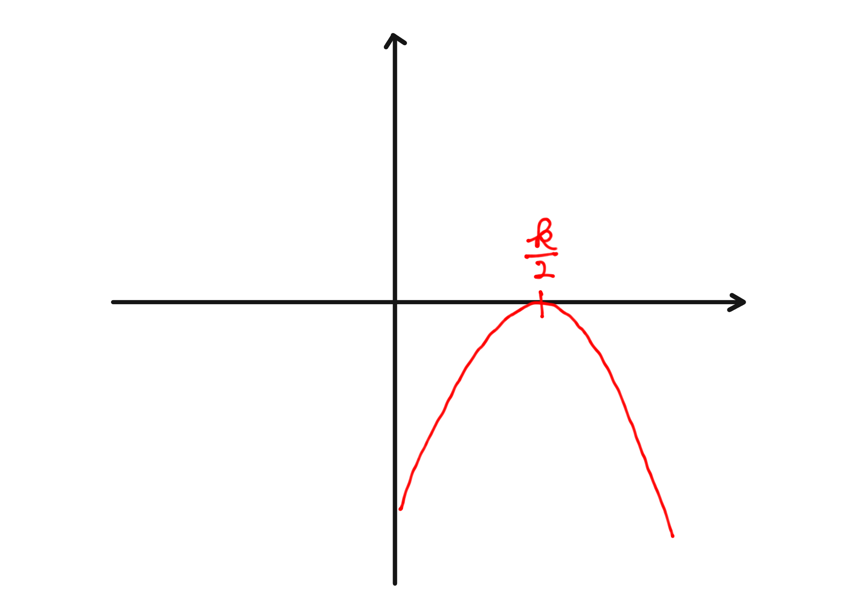
これは,判別式を $D$ として,
$$\frac{D}{4}=k^2-(-2)(k-3)=k^2+2k-6=0,$$
すなわち,
$$k=-1+\sqrt{7},-1-\sqrt{7}.$$
$0\leqq t<1$ で解を持つので,
$$0\leqq \frac{k}{2}<1$$
となる必要がある。
よって,
$$0\leqq k<2$$
であるので,
$$k=-1+\sqrt{7}.$$
(2) 図のように $f(0)\geqq0$ かつ $f(1)<1$
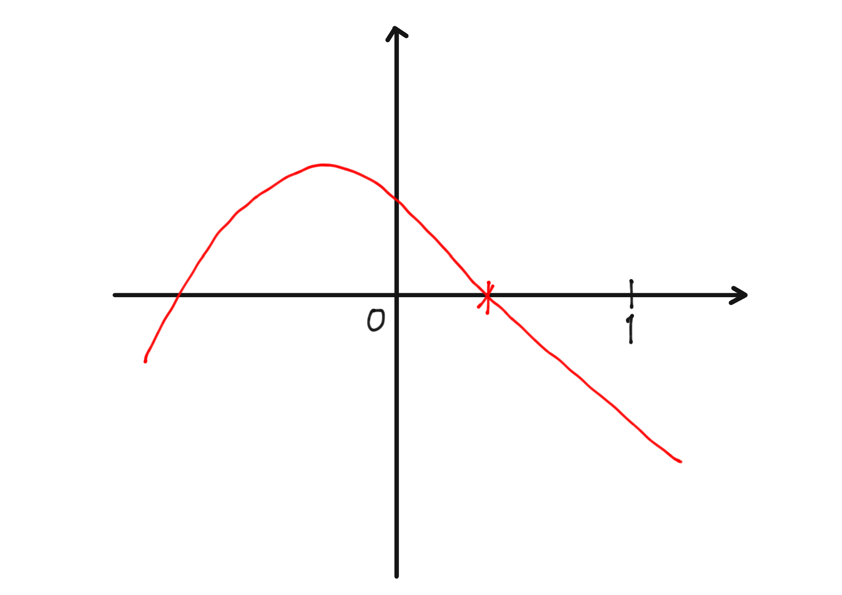
$$f(0)=k-3\geqq0~~\text{かつ}~~f(1)=3k-5<0.$$
よって,
$$k\geqq3~~\text{かつ}~~k<\frac{5}{3}.$$
これは不適。
(3)図のように $f(0)\leqq0$ かつ $f(1)>0$
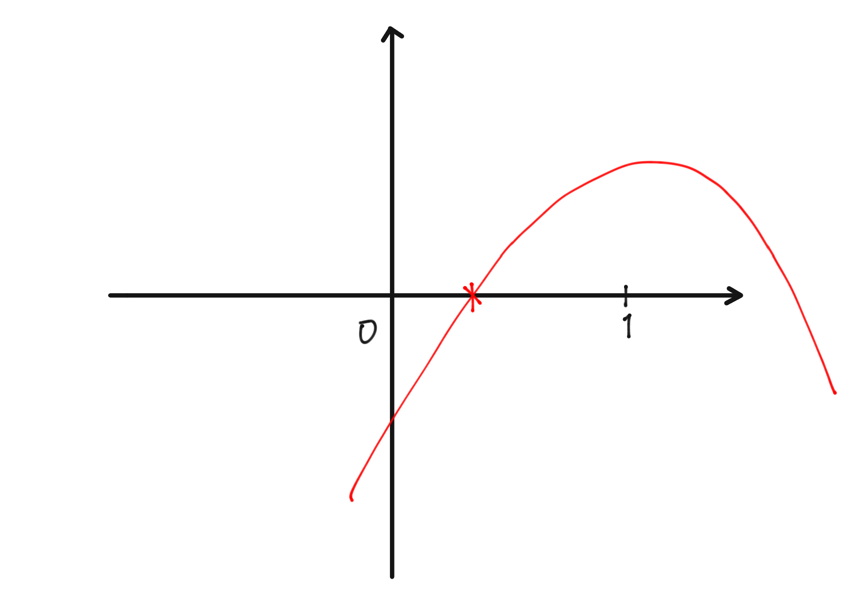
$$f(0)=k-3\leqq0~~\text{かつ}~~f(1)=3k-5>0.$$
よって,
$$k\leqq3~~\text{かつ}~~k>\frac{5}{3}.$$
よって,
$$\frac{5}{3}<k\leqq 3.$$
$(1)\sim(3)$より,
$$k=-1+\sqrt{7},~~\frac{5}{3}<k\leqq 3.$$


