こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

今日は直線と領域の問題です。
今日は例題を理解してから問題に取り組もう!
例題
実数 $m$ の値が変化するとき,直線 $y=2mx-m^2$ が通る領域を図示せよ。
例題の解答
$m$ の値が変わるので,与式を整理すると
$$m^2-2xm+y=0.$$
実数 $m$ が存在するためには判別式を $D$ として,
$$\frac{D}{4}=x^2-1\cdot y\geqq 0.$$
よって,
$$y\leqq x^2.$$
この式を満たす $(x,y)$ に対して
$$y=2mx-m^2$$
を満たす実数 $m$ が存在するので,
この点 $(x,y)$ は与えられた直線上にある。
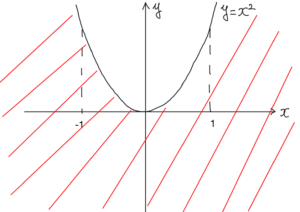
よって,求める領域は図の斜線部分である。
ただし,境界を含む。
問題
$x$ 軸上を動く点 $P$ がある。このとき,点 $A(2,1)$ と点 $P$ を結ぶ線分 $AP$ の垂直2等分線が通らない領域を図示せよ。
問題の解答
まずは,$AP$ の垂直2等分線を求める。
$P$ は $x$ 軸上にあるので,
$$(m,0)$$
とおくことができる。
よって,線分 $AP$ の中点は
$$\left(\frac{m+2}{2},\frac{0+1}{2}\right)=\left(\frac{m+2}{2},\frac{1}{2}\right).$$
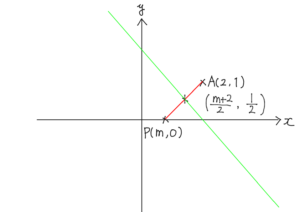
点$A$, $P$ を通る直線の傾きは
$$\frac{1-0}{2-m}=\frac{1}{2-m}$$
よって,垂直2等分線の傾き $a$ は
$$a\cdot \frac{1}{2-m}=-1$$
よって,
$$a=m-2.$$
よって,垂直2等分線は
\begin{align*}
y-\frac{1}{2}
&=(m-2)\left(x-\frac{m+2}{2}\right)\\
&=(m-2)x-\frac{(m-2)(m+2)}{2}\\
&=mx-2x-\frac{m^2-4}{2}\\
\end{align*}
よって,
$$m^2-2xm+\left(2y-1+4x-4\right)=0,$$
$$m^2-2xm+\left(2y+4x-5\right)=0.$$
判別式を $D$ とすると,求める領域は垂直2等分線が通らない領域なので,
$m$ が存在しない領域,すなわち,
$$\frac{D}{4}=x^2-\left(2y+4x-5\right)<0.$$
よって,
\begin{align*}
y >& \frac{1}{2}x^2-2x+\frac{5}{2}\\
=& \frac{1}{2}(x^2-4x)+\frac{5}{2}\\
=& \frac{1}{2}(x-2)^2-\frac{1}{2}\cdot 4+\frac{5}{2}\\
=& \frac{1}{2}(x-2)^2+\frac{1}{2}.
\end{align*}
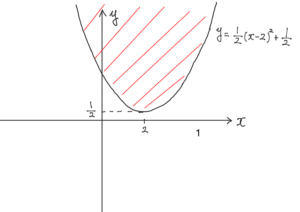
よって,求める領域は図の斜線部分である。
ただし,境界線は含まない。