こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

今日は指数関数の方程式が解を持つための条件の問題です。
指数関数独特の問題だよ。
問題
$x$ についての方程式
$$\log_a(x-2)-\log_a(x+1)-\log_a(x-1)=1$$
が解をもつような定数 $a$ の値の範囲を求めよ。
解答
真数条件より
$$x-2>0,~~x+1>0,~~x-1>0.$$
よって,
$$x>2,~~x>-1,~~x>1.$$
よって,
$$x>2.$$
底の条件より,
$$a>0,~~a\not=1.$$
$$\log_a(x-2)-\log_a(x+1)-\log_a(x-1)=1$$
を式変形して,
$$\log_a\Big(\frac{x-2}{(x+1)(x-1)}\Big)=1.$$
よって,
$$\frac{x-2}{x^2-1}=a^1=a.$$
よって,
$$x-2=a(x^2-1).$$
よって,
$$ax^2-x-a+2=0.$$
後はこの2次方程式が
$x>2,a>0,a\not=1$
のもとで解を持つための条件を求めればよい。
$$f(x)=ax^2-x-a+2$$
とおく。$x>2$ の範囲を考えるので,$x=2$ のときの $f(x)$ の値を求めると,
$$f(2)=4a-2-a+2=3a.$$
$a>0$ より,
$$ax^2-x-a+2=0$$
が解を持つのは図のようになる場合である。
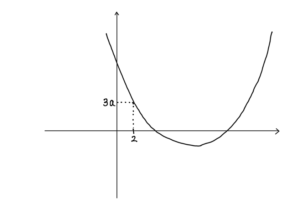
よって,
\begin{align*}
f(x)
=&~ax^2-x-a+2\\
=&~a\Big(x^2-\frac{1}{a}x\Big)-a+2\\
=&~a\Big(x-\frac{1}{2a}\Big)^2-a\cdot\frac{1}{4a^2}-a+2\\
=&~a\Big(x-\frac{1}{2a}\Big)^2{\color{red}-\frac{1}{4a}-a+2}
\end{align*}
つまり,
$${\color{red}-\frac{1}{4a}-a+2}\leqq0$$
となればよい。両辺 $-4a$ をかけて
$$1+4a^2-8a\geqq0.$$
よって,
$$4a^2-8a+1\geqq0.$$
$$4a^2-8a+1=0$$
を解くと
$$a=\frac{4\pm\sqrt{4^2-4\cdot1}}{4}=\frac{4\pm2\sqrt{3}}{4}=\frac{2\pm\sqrt{3}}{2}.$$
よって,図より,
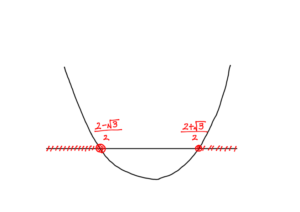
$$a\leqq\frac{2-\sqrt{3}}{2},~~\frac{2+\sqrt{3}}{2}\leqq a.$$
また,$2<\frac{1}{2a}$より,
$$a<\frac{1}{4}.$$
よって,条件を全てかくと,
$$a>0,~~a\not=1,~~a<\frac{1}{4},~~a\leqq\frac{2-\sqrt{3}}{2},~~\frac{2+\sqrt{3}}{2}\leqq a.$$
よって,
$$0<a\leqq\frac{2-\sqrt{3}}{2}.$$



コメント