こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

今日は指数関数の不等式の問題だよ。
これができれば,指数関数はOK!
問題
方程式 $4^x-a\cdot 2^{x+1}+2a+3=0$ を満たす実数 $x$ が存在するような実数 $a$ の値の範囲を求めよ。
解答
${\color{red}2^x=t}$ とおくと,
$$4^x-a\cdot 2^{x+1}+2a+3=t^2-2at+2a+3.$$
これを
$$f(t)=t^2-2at+2a+3$$
とおく。求めたいのは
$f(t)=0$ が $t=2^x>0$ に解を持つための条件。
これは
$y=f(t)$
のグラフと $t$ 軸が $t>0$ の範囲で共有点を持てばよい。
次のいずれかで場合わけをする。
(i) $f(0)<0$ のとき,(ii) $f(0)\geqq0$ のとき
(i) $f(0)<0$ のとき
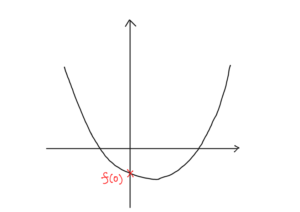
図より,常に解を持つ。
条件は
$$f(0)=2a+3<0.$$
よって,
$$a<-\frac{3}{2}.$$
(ii) $f(0)\geqq0$ のとき
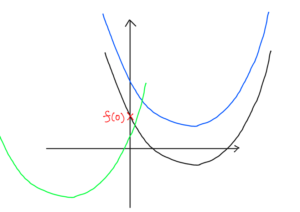
図より,緑と青の場合は起こり得ない。
黒の場合のみ起こり得る。
つまり,条件は
$f(0)\geqq0$,
かつ
$f(t)=0$ の判別式を $D$ として,
$$D\geqq0$$
かつ,
$$\text{軸が}0\text{より大きい。すなわち,}t=a>0.$$
$f(0)\geqq0$より,
$$f(0)=2a+3\geqq0.$$
よって,
$$a\geqq-\frac{3}{2}\tag{1}$$
$D\geqq0$ より,
$$\frac{D}{4}=a^2-(2a+3)=(a+1)(a-3)\geqq0.$$
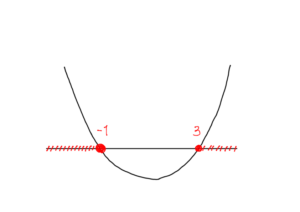
図より,
$$a\leqq-1,~~3\leqq a \tag{2}$$
軸について,
$$t=a>0\tag{3}.$$
よって,(1), (2), (3) より
$$a\geqq3.$$
(i), (ii) より,
$$a<-\frac{3}{2},~~a\geqq3.$$


