こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

これが解ければ,軌跡はいい感じ!
今日はじっくり1問!
問題
放物線 $y=x^2$ と直線 $y=mx-3$ が異なる2点 $P,~Q$ で交わるとき,線分 $P,~Q$ の中点 $R$ の軌跡を求めよ。
問題の解答
求める点を $(X,Y)$ とおく。
$(X,Y)$ は $P,~Q$ の中点より,
$P$ を $(x_1,y_1)$, $Q$ を $(x_2,y_2)$ とおくと,
$$X=\frac{x_1+x_2}{2},~~Y=\frac{y_1+y_2}{2}.$$
$P,~Q$ は $y=x^2$ と $y=mx-3$ の異なる2点の交点より,
\begin{align*}
mx-3=x^2,\\
x^2-mx+3=0
\end{align*}
の異なる2つの解。
解と係数の関係より,
\begin{equation}
x_1+x_2=m,~~x_1x_2=3.
\end{equation}
よって,
$$\frac{X}{2}=m,$$
よって,
\begin{equation}
2X=m. \tag{1}
\end{equation}
$X$ と $Y$ の関係を考えたい。
$(x_1,y_1)$, $(x_2,y_2)$ は
$$y_1=x_1^2,~~y_2=x_2^2,$$
$$y_1=mx_1-3,~~y_2=mx_2-3$$
を満たすので,
$$y_1+y_2=m(x_1+x_2)-6.$$
よって,
$$2Y=2mX-6,$$
$$Y=mX-3.$$
これに (1) を代入して,
$$Y=2X^2-3.$$
$X$ の動く範囲を考える。
$$x^2-mx+3=0$$
の判別式を $D$ として,
$$D=m^2-4\cdot 3=m^2-12=(m-2\sqrt{3})(m+2\sqrt{3})>0$$
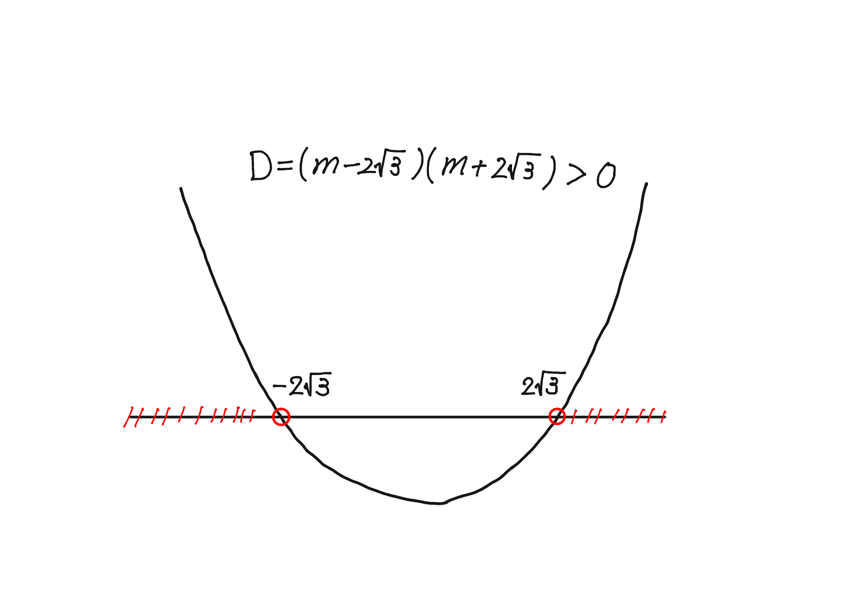
図より,
$$m<-2\sqrt{3},~~2\sqrt{3}<m.$$
よって,
$$2X<-2\sqrt{3},~~2\sqrt{3}<2X.$$
よって,
$$X<-\sqrt{3},~~\sqrt{3}<X.$$
よって,求める軌跡は
$$y=2x^2-3,$$
ただし,$x<-\sqrt{3},~~\sqrt{3}<x$ の部分。
今日のポイント
2. 中点 $\frac{x_1+x_2}{2}$ には $x_1+x_2$ が出てくるので,
解の足し算(掛け算)といえば解と係数の関係!
頭を良くしたいならDHAがおすすめです↓



