こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

今日は不等式の表す領域の問題だよ。
図をかきながら考えよう。
問題
3点 $A(-1,2),~B(4,1),~C(1,5)$ を頂点とする $\triangle ABC$ の内部および周を表す不等式を求めよ。
点 $(x,y)$ が問題1の $\triangle ABC$ の内部及び周上を動くとき,
$2x+y$
の最大値と最小値を求めよ。
点 $(x,y)$ が問題1の $\triangle ABC$ の内部及び周上を動くとき,
$x^2+y^2$
の最大値と最小値を求めよ。
解答
問題1の解答
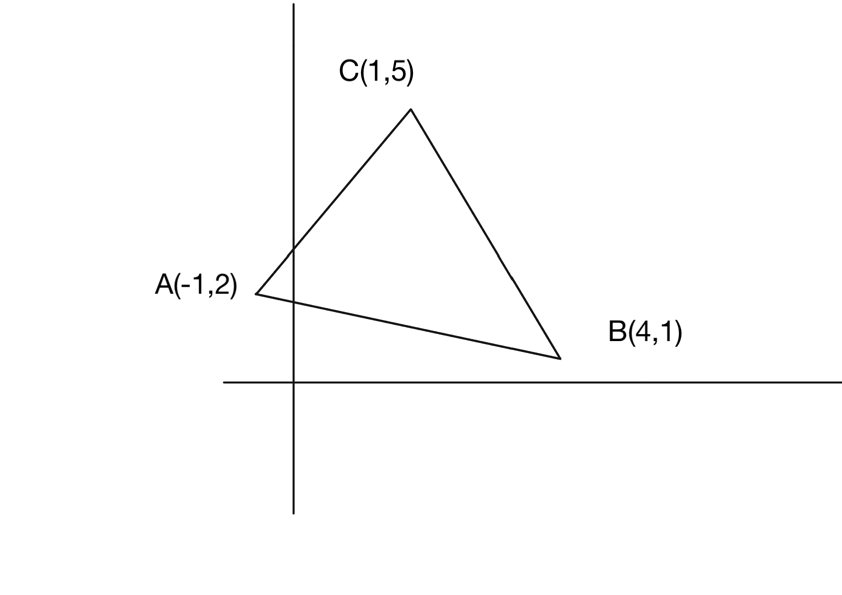
図のように $\triangle ABC$ の内部及び周上は直線 $AB,~BC,~CA$ で囲まれる領域である。
直線 $AB$ は
$$y=-\frac{1}{5}x+\frac{9}{5},$$
直線 $BC$ は
$$y=-\frac{4}{3}x+\frac{19}{3},$$
直線 $CA$ は
$$y=\frac{3}{2}x+\frac{7}{2}.$$
よって,$\triangle ABC$ の内部及び周を表す不等式は
$$y\geq-\frac{1}{5}x+\frac{9}{5},
~~y\leq-\frac{4}{3}x+\frac{19}{3},
~~y\leq\frac{3}{2}x+\frac{7}{2}.$$
問題2の解答

問題2をもう1度確認
点 $(x,y)$ が問題1の $\triangle ABC$ の内部及び周上を動くとき,
$2x+y$
の最大値と最小値を求めよ。
問題2の解答
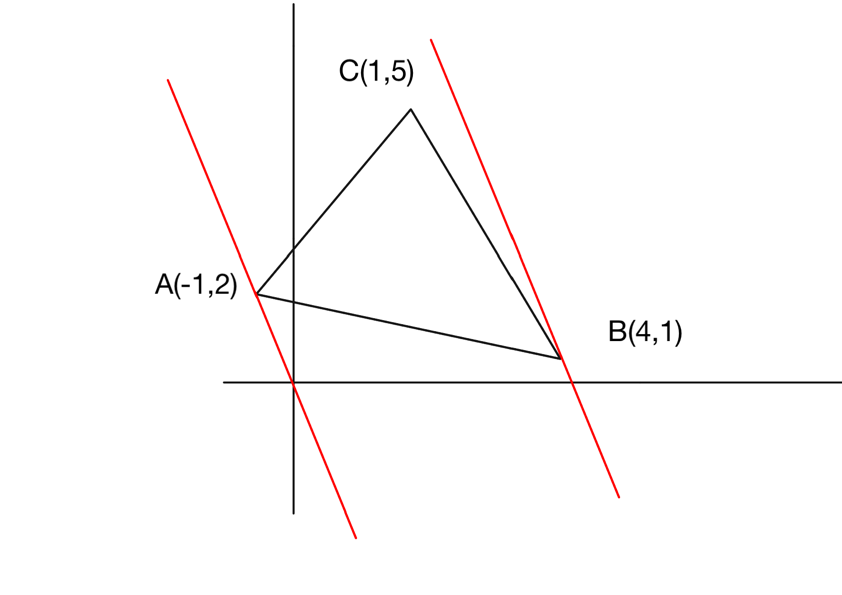
${\color{red} 2x+y=k}$ とおく。
$$y=-2x+k$$
の $k$ が最大値となるのは図より,
点 $B$ を通るとき。
よって,
$B(4,1)$ を代入して,
$$k=2\cdot 4+1=9.$$
$$y=-2x+k$$
の $k$ が最小値となるのは図より,
点 $A$ を通るとき。
よって,
$A(-1,2)$ を代入して,
$$k=2\cdot (-1)+2=0.$$
以上より,最大値 $9$, 最小値 $0.$
問題3の解答

問題3をもう1度確認
点 $(x,y)$ が問題1の $\triangle ABC$ の内部及び周上を動くとき,
$x^2+y^2$
の最大値と最小値を求めよ。
問題3の解答
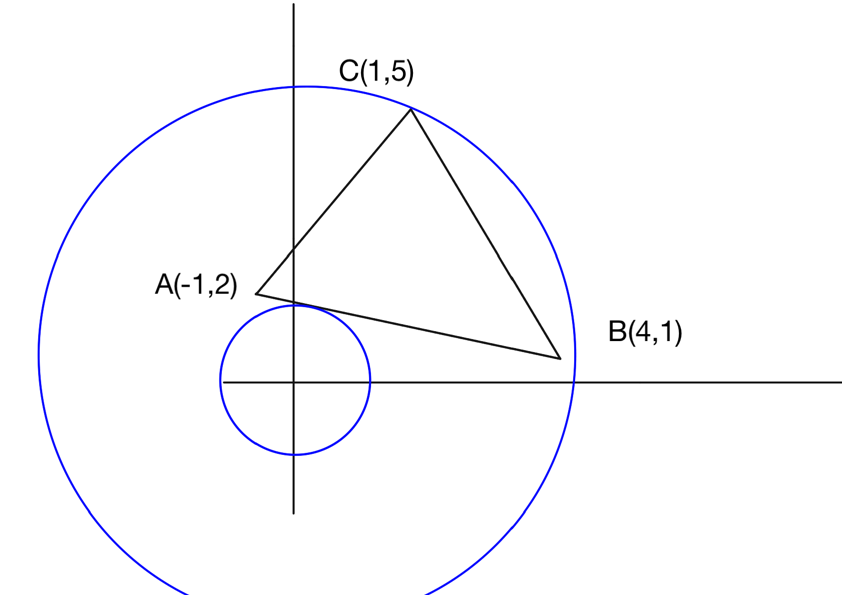
${\color{red}x^2+y^2=k}$とおく。
$k$ が最大となるのは図より,
点$C$ を通るときより,
$C(1,5)$ を代入して,
$$k=1^2+5^2=26.$$
$k$ が最小となるのは図より,
直線 $AB$ と接するときより,
点 $O$ と 直線 $AB$ との距離を求める。
直線 $AB$ は
$$x+5y-9=0$$
とかけるので,
点と直線の距離の公式より
$$\frac{|1\cdot 0+5\cdot 0-9|}{\sqrt{1^2+5^2}}=\frac{9}{\sqrt{26}}.$$
よって,
$$k=\left(\frac{9}{\sqrt{26}}\right)^2=\frac{81}{26}.$$
よって,最大値 $26$, 最小値 $\frac{81}{26}$.



