こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

今日は三角関数の問題だよ。
今日は難問。
じっくり考えていこう!
問題
$0^\circ \leqq \theta< 360^\circ$ のとき,方程式
$$\sin^2\theta+a\sin\theta+b=0$$
を満たす $\theta$ が存在するための,$(a,b)$ の領域を図示せよ。
解答
$x=\sin\theta$ とおく。
このとき,2次方程式
$$x^2+ax+b=0$$
が $-1\leqq x\leqq1$ ($-1\leqq \sin\theta\leqq1$より)
で解を持てばよい。
$f(x)=x^2+ax+b$
とおく。
$f(x)=0$ が
$-1\leqq x\leqq1$ が解を持つ場合を考える。
( i ) $f(-1)=1-a+b\leqq 0$ かつ $f(1)=1+a+b\geqq0$ のときは必ず解を持つ。
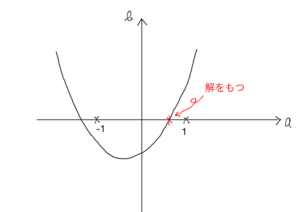
よって,$b\leqq a-1$ かつ $b\geqq -a-1$ のとき解を持つ。
( ii ) $f(-1)=1-a+b\geqq 0$ かつ $f(1)=1+a+b\leqq0$ のときは必ず解を持つ。
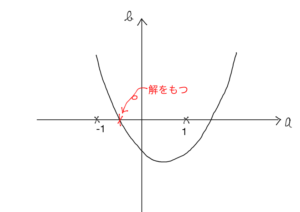
よって,
$b\geqq a-1$ かつ $b\leqq-a-1$ のとき解を持つ。
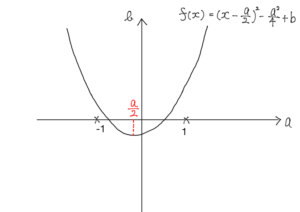
( iii ) $f(-1)=1-a+b\geqq 0$ かつ $f(1)=1+a+b\geqq 0$ のときを考える。
下図より,
$-1\leqq\frac{a}{2}\leqq1.$
$f(x)=0$ の判別式を $D$ として,
$$D=a^2-4b\geqq0.$$
よって,
$$b\leqq\frac{a^2}{4}.$$
よって,
\begin{cases}
b\leqq\frac{a^2}{4},\\
-2\leqq a\leqq 2,\\
b\geqq a-1,\\
b\geqq -a-1.
\end{cases}
のとき,解を持つ。
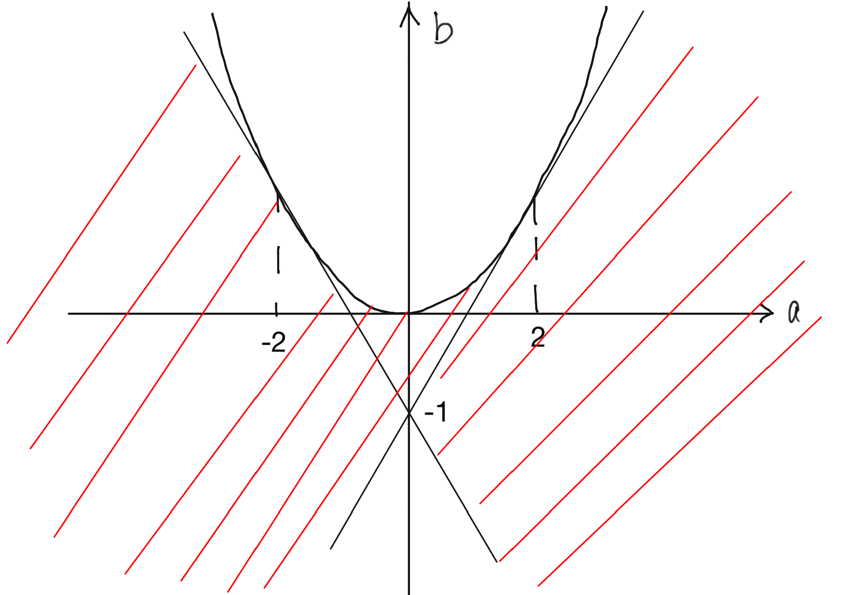
よって,( i ), ( ii ), ( iii ) より,求める領域は下図のようになる。
ただし,境界線を含む。