こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

今日は不等式の表す領域の問題だよ。
今日はじっくり考える問題だよ!
問題
2次方程式 $x^2-2ax+b=0$ が異なる2つの解を持つとする。
この2つの解がともに $-1\leqq x\leqq 1$ の範囲にあるような,
点 $(a,b)$ の存在範囲を図示せよ。
不等式 $x^2+y^2\leqq 4$ の表す領域内を点 $(x,y)$ が動くとき,
$X=x+y$, $Y=xy$ として,点 $(X,Y)$ の存在する領域を図示せよ。
解答
問題1の解答
$f(x)=x^2-2ax+b=(x-a)^2-a^2+b$ とおく。
2次方程式 $f(x)=0$ の2つの解がともに$-1\leqq x\leqq 1$ の範囲にあるのは
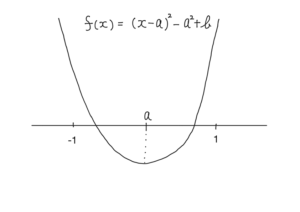
条件は
\begin{equation*}
\left\{
\begin{aligned}
&-1<a<1\\
&f(a)=-a^2+b<0\\
&f(-1)=1+2a+b\geqq0\\
&f(a)=1-2a+b\geqq0\\
\end{aligned}
\right.
\end{equation*}
すなわち,
\begin{equation*}
\left\{
\begin{aligned}
&-1<a<1\\
&b<a^2\\
&b\geqq 2a-1\\
&b\geqq -2a-1\\
\end{aligned}
\right.
\end{equation*}
これを満たす点 $(a,b)$ の存在範囲は
下図の射線部分。
ただし,境界は
$$b=a^2$$
の放物線は含まず,そのほかの境界は含む。

問題2の解答

まずは問題を確認
不等式 $x^2+y^2\leqq 4$ の表す領域内を点 $(x,y)$ が動くとき,
$X=x+y$, $Y=xy$ として,点 $(X,Y)$ の存在する領域を図示せよ。
$X=x+y$, $Y=xy$
より,
$$x^2+y^2=(x+y)^2-2xy=X^2-2Y.$$
よって,
$$x^2+y^2\leqq 4$$
より,
$$X^2-2Y\leqq 4,$$
$$Y\geqq \frac{1}{2}X^2-2.$$
ここで,$x,~y$ が存在する条件を書く。
$x,~y$ を2つの解にもつ2次方程式は
$$(t-x)(t-y)=0$$
で
$$t^2-(x+y)t+xy=0,$$
すなわち,
$$t^2-Xt+Y=0.$$
判別式を $D$ とすると
$$D=X^2-4Y\geqq0.$$
よって,
$$Y\leqq \frac{1}{4}X^2.$$
以上より,求める領域は
$$Y\geqq \frac{1}{2}X^2-2$$
かつ
$$Y\leqq \frac{1}{4}X^2.$$
すなわち,下図のようになる。
ただし,境界線を含む。




