こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」
今日も楽しんでいきましょう!

今日は円に関する問題だよ。
1問で2問分勉強できるいい問題だよ。
問題
$m$を定数とする。方程式
$$x^2+y^2+2mx-6y+3m^2+4m+3=0$$
が円を表すとき,次の問いに答えよ。
(1) 定数$m$の値の範囲を求めよ。
(2) この円の半径の最大値を求めよ。
解答
(1)の解答
問題1(1)の解答
(1) 方程式
$$x^2+y^2+2mx-6y+3m^2+4m+3=0$$
を変形する。
\begin{align*}
&~x^2+y^2+2mx-6y+3m^2+4m+3\\
&=~ x^2+2mx+y^2-6y+3m^2+4m+3\\
&=~ (x+m)^2{\color{red}-m^2}+(y-3)^2{\color{red}-9}+3m^2+4m+3\\
&=~ (x+m)^2+(y-3)^2+2m^2+4m-6.\\
\end{align*}
よって,方程式は
$$(x+m)^2+(y-3)^2+2m^2+4m-6=0.$$
よって,
$$(x+m)^2+(y-3)^2=-2m^2-4m+6.$$
よって,中心$(-m,3)$,半径 $\sqrt{-2m^2-4m+6}$ の円。
円の半径は0より大きいので,
\begin{align*}
-2m^2-4m+6&>0.\\
-2(m^2+2m-3)&>0.\\
m^2+2m-3&<0\\
(m+3)(m-1)&<0
\end{align*}
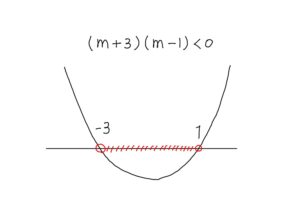
よって,
$$m<-3,~~1<m.$$

不等式が出てきたら必ず,図をかこう!
(2)の解答
(1) より,半径は $\sqrt{-2m^2-4m+6}.$
よって,
$$-2m^2-4m+6$$
の最大値を求める。
\begin{align*}
-2m^2-4m+6
=&~-2(m^2+2m)+6\\
=&~-2\{(m+1)^2-1\}+6\\
=&~-2\{(m+1)^2+8\\
\end{align*}
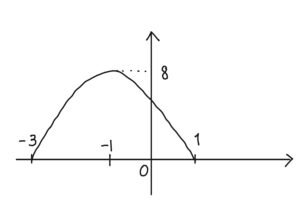
よって,図より,$-3<m<1$において $-2m^2-4m+6$ の最大値は
$m=-1$ のとき,$8.$
よって,半径 $\sqrt{-2m^2-4m+6}$ の最大値は
$m=-1$ のとき,$\sqrt{8}=2\sqrt{2}.$
今日のポイント
$$(x-a)^2+(y-b)^2=r^2.$$
頭を良くしたいならDHAがおすすめです↓



