こんにちは。脱サラ数学者の妻たーこです。
「わかりやすい高校数学」。
今日も楽しんでいきましょう!

円と直線についての問題だよ。
問題
$a$ を定数とする。円 $x^2+y^2=5$ と直線 $y=2x+a$ の共有点の個数を求めよ。
$a$ を定数とする。円 $x^2+y^2=5$ と直線 $y=ax-3$ の共有点の個数を求めよ。
解答
問題1の解答
$x^2+y^2=5$ に $y=2x+a$ を代入して
\begin{align*}
x^2+(2x+a)^2=&~ 5\\
x^2+4x^2+4ax+a^2=&~ 5\\
5x^2+4ax+a^2-5=&~ 0.\\
\end{align*}
判別式を $D$ として,
$$\frac{D}{4}=4a^2-5(a^2-5)=-a^2+25=-(a^2-25)=-(a+5)(a-5).$$
よって,$-(a+5)(a-5)>0$ のとき,
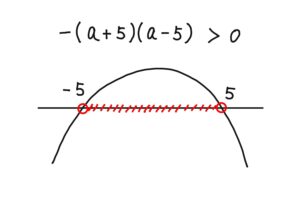
すなわち,$\boldsymbol{-5<a<5}$ のとき,共有点2個。
$-(a+5)(a-5)=0$ のとき,すなわち,
$\boldsymbol{a=\pm5}$のとき,共有点1個。
$-(a+5)(a-5)<0$ のとき,
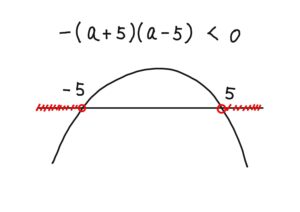
すなわち,$\boldsymbol{a<-5,~5<a}$ のとき,共有点0個。
問題2の解答
$x^2+y^2=5$ に $y=ax-3$ を代入して
\begin{align*}
x^2+(ax-3)^2=&~ 5\\
x^2+a^2x^2-6ax+9=&~ 5\\
(a^2+1)x^2-6ax+4=&~ 0.\\
\end{align*}
判別式を $D$ として,
$$\frac{D}{4}=9a^2-(a^2+1)4=5a^2-4=5\Big(a^2-\frac{4}{5}\Big)=5\Big(a+\frac{2\sqrt{5}}{5}\Big)\Big(a-\frac{2\sqrt{5}}{5}\Big).$$
よって,$\Big(a+\frac{2\sqrt{5}}{5}\Big)\Big(a-\frac{2\sqrt{5}}{5}\Big)>0$ のとき,
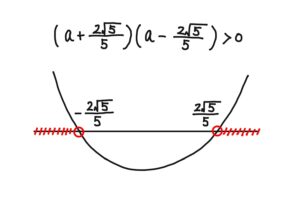
すなわち,$\boldsymbol{a<-\frac{2\sqrt{5}}{5},~\frac{2\sqrt{5}}{5}<a}$ のとき,共有点2個。
$\Big(a+\frac{2\sqrt{5}}{5}\Big)\Big(a-\frac{2\sqrt{5}}{5}\Big)=0$ のとき,すなわち,
$\boldsymbol{a=\pm \frac{2\sqrt{5}}{5}}$のとき,共有点1個。
$\Big(a+\frac{2\sqrt{5}}{5}\Big)\Big(a-\frac{2\sqrt{5}}{5}\Big)<0$ のとき,
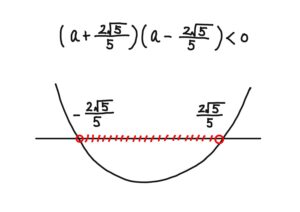
すなわち,$\boldsymbol{-\frac{2\sqrt{5}}{5}<a<\frac{2\sqrt{5}}{5}}$ のとき,共有点0個。
今日のポイント
(2) 判別式で出てくる「不等式は必ず絵をかくこと」
頭を良くしたいならDHAがおすすめです↓



